이상엽 선형대수학 정주행 1회차 - 행렬의 기본

1. 기본 용어 정리

• 행렬(Matrix): 다수의 수를 직사각형의 형태로 배열한 것 
• 성분(Elemnt): 행렬에 배열된 구성원
• 행(Row): 행렬의 가로줄
• 열(Column): 행렬의 세로줄
• m x n 행렬: m개의 행과 n개의 열로 이루어진 행렬
• 주대각선(Main Diagonal): 행렬의 왼쪽 위에서 오른쪽 아래를 가르는 선
• 대각성분(Diagonal Elements): 행과 열의 지표수가 같은 성분 - (1, 1), (2, 2) ...

5 x 4 행렬. 5개의 행과 4개의 열로 이루어져 있다.

TMI: C언어에서 2차원 배열 int arr[x][y]; 에서 사실 x가 세로 길이였던 것이 기억나는가? 사실 나는 "왜 헷갈리게 앞의 것을 가로 길이가 아니라 세로 길이라고 해놓은거야?!" 라는 불평을 했는데 사실 세로 길이가 아니라 행의 갯수였던 것이다!

 

2. 행렬의 종류

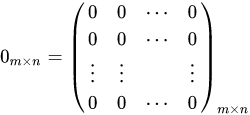
1) 영행렬(Zero Matrix or Null Matrix): 모든 성분이 0인 행렬

모든 원소가 0이다.

 

2) 전치행렬(Transpose Matrix): 어떤 행렬의 행과 열을 바꿔서 얻어낸 행렬

대문자 T로 표시한다.

 

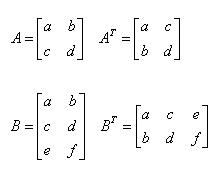
3) 대칭행렬(Symmetric Matrix): 어떤 행렬을 전치행렬로 만들었을 때, 초기의 행렬과 같은 행렬

주대각선을 기준으로 서로 대칭이다.

 

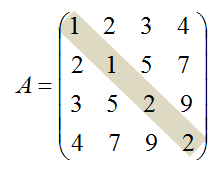
4) 반대칭행렬(Skew-Symmetrix Matrix): 전치행렬이 덧셈 역원과 같은 행렬

전치행렬과 더하면 영행렬이 나오며 대각성분이 모두 0이다.

 

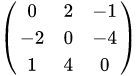
5) 정사각행렬(Square Matrix): 행, 열의 갯수가 같은 행렬

행, 열의 수가 3개로 같다.

 

6) 대각행렬(Diagonal Matrix): 대각성분을 제외한 모든 성분이 0인 정사각행렬

대각성분이외의 모든 성분은 0이다.

 

7) 단위행렬(Identity Matrix): 모든 대각 성분이 1이고 나머지 성분은 0인 정사각행렬

항등행렬이라고도 부른다.

 

 

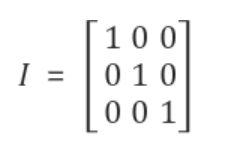
3. 행렬의 연산

1) 행렬의 덧셈 및 뺄셈

일반적인 행렬의 덧셈과 뺄셈은 매우 직관적이어서 어떻게 더하고 빼는지 한 번 알면 바로 기억하기 쉬우며 행렬의 크기가 서로 다른 상태에서는 더하거나 뺄 수 없기 때문에 주의해야 한다. 덧셈과 뺄셈이 이루어지는 방식은 아래와 같이 그냥 각자 같은 위치에 있는 성분들끼리 더하거나 빼면 된다.

해치웠나? (1트)

 

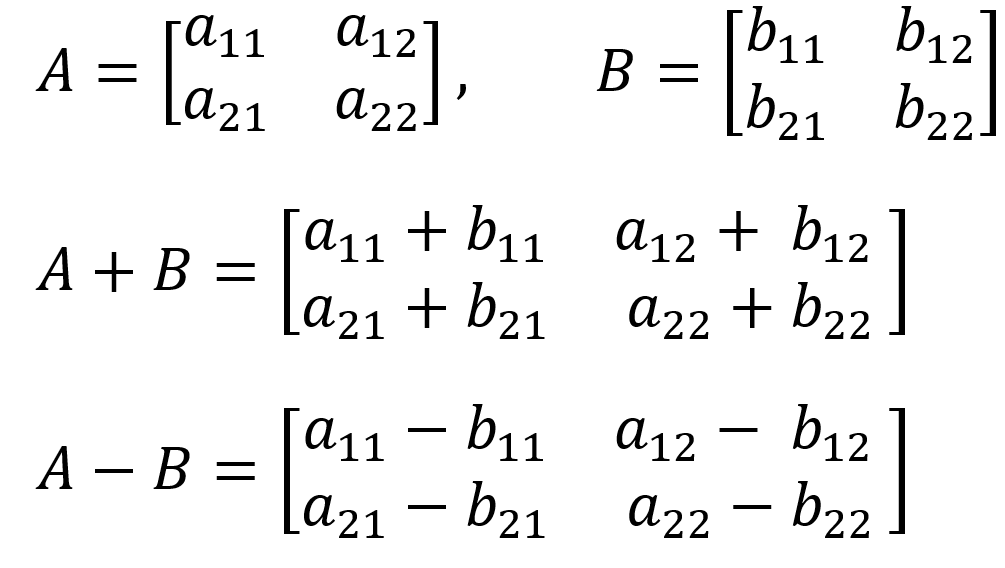
2) 행렬의 스칼라곱

얘는 덧셈, 뺄셈보다 더 쉽다. 그냥 행렬의 모든 성분을 곱하고자 하는 수만큼 곱해주면 된다. 상수배한다고 생각하면 된다. 더 설명할 것이 없다.

해치웠나?! (2트)

 

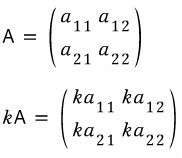
3) 행렬의 곱셈

어떤 놈이 마법의 주문을 무려 2번이나 외우는 바람에 이 부분부터 좀 어려워진다. 우선 행렬의 곱셈이 성립하려면 아래의 이미지처럼 앞의 행렬의 열의 갯수와 뒤의 행렬의 행의 갯수가 같아야 한다. 그래야 곱셈이 가능하며 이 부분은 "왜?" 라고 하기에는 그냥 행렬의 곱셈의 정의가 이렇기 때문에 뭐라고 대답할 방법이 없다... 행렬의 곱셈이 이루어지면 아래의 이미지처럼 앞의 행렬의 행의 갯수와 뒤의 행렬의 열의 갯수만큼의 크기를 가진 행렬이 나오게 된다.

길이와 갯수를 헷갈리지 말자. 마치 길이인 것처럼 되어있지만 갯수라는 것을 인지하자.

아무튼 이렇게 m개의 행과 k개의 열을 가진 행렬과 k개의 행과 n개의 열을 가진 행렬을 곱하면 m개의 행과 n개의 열을 가진 행렬이 나오게 된다. 이제 행렬의 곱셈이 이루어지는 과정을 보자.

규칙이 보이는가?

앞의 행렬의 행의 방향과 뒤의 행렬의 열의 방향의 성분들을 순서대로 곱하고 전부 더해주고 있는 모습을 볼 수 있다. 바로 이런 행렬의 곱셈 과정에 의해서 각 행렬의 행과 열의 갯수가 위에서 말한 것처럼 맞아 떨어져야 한다. 지금같은 경우는 각각 2 x 2행렬끼리 곱했으니 그 결과도 2 x 2행렬이 나오게 된다.

 

"따라서 행렬의 곱셈은 교환 법칙이 성립하지 않는다."

 

절대 헷갈리지 말자. 행렬의 곱셈 연산을 하는데 무심코 교환 법칙을 하려고 할 수 있다. 주의해야 한다.