2023. 4. 3. 15:30ㆍ집합론
1. 명제와 증명
수학은 흔히 논리적인 학문이라고 말한다. 그리고 수학에서 논리는 명제로부터 비롯된다. 그만큼 수학을 공부하는데 있어서 명제는 절대 빼놓을 수 없는 요소인 것이다. 그럼 명제에 대해서 알아보자.
1) 명제와 연결사
명제의 일반적인 정의는 참, 거짓이 분명히 구분되는 문장이라고 정의한다. 다만 이전 글에서 말했듯이 이 상식은 집합론을 배우면서 산산조각이 날테니 우선 이렇게 알고 넘어가자. 당분간은 적용이 가능하니 말이다.
단순 명제 - ex: 1은 자연수이다. (명제) / 서울 집 값은 비싸다. (명제 아님)
말 그대로 "A는 B이다." 와 같은 형식의 문장들 중 수학적으로 명확하게 참과 거짓을 구분할 수 있는 문장을 말한다. 다만 위에서 "서울 집 값이 비싸다." 라고 하는 것이 명제가 아니라고 했는데 비싸다는 기준이 제시되어 있지 않기 때문이다.
합성 명제 - ex: 1은 자연수이고 0.5는 소수이다.
합성 명제는 2개 이상의 단순 명제로 이루어진 명제를 의미한다. 간단한 내용이니 간단하게 이해하고 넘어가면 된다.
연결사: 1개 이상의 명제를 연결해주는 단어
| 명 칭 | 기 호 | 읽는 법 |
| 부 정 | ~p | not p |
| 논리곱 | p ∧ q | p and q |
| 논리합 | p ∨ q | p or q |
| 조 건 | p → q | if p, then q |
| 쌍조건 | p ↔ q | p if and only if q |
C++을 배운 사람이라면 위의 표가 굉장히 익숙할 것이다. 그곳에도 not, and, or 연산자는 얼마든지 있을 뿐더러 if문도 여러 번 작성해 봤을테니 말이다. 그러니까 그냥 이런 기호가 있나보다 하고 넘어가면 된다.
2) 진리표
명제의 진리값을 표로 나타낸 것으로 여기서 진리값은 참, 거짓을 의미한다. 진리집합이라는 것도 있는데 어떤 명제가 참이 되도록 만드는 원소들의 집합을 의미한다. 표기는 어떤 명제를 소문자 알파벳으로 표기할 때, 해당 명제의 진리집합은 해당 알파벳의 대문자로 표기한다. 아래는 p, q에 대한 진리표를 나타낸다. 그렇게 어려운 내용이 아니어서 차근차근 이해하면 어렵지 않게 넘어갈 수 있을 것이다.
| p q | ~p | p ∧ q | p ∨ q | p → q | p ↔ q |
| T T | F | T | T | T | T |
| T F | F | T | F | F | |
| F T | T | F | T | T | F |
| F F | F | F | T | T |
이제 아래 5개의 명제에 대해 진리표를 작성할 것이다. 모두 자주 쓰이는 동치관계이니 알아두면 좋다.
① p → q ≡ ~p ∨ q
| p q | p → q | ~p ∨ q |
| T T | T | T |
| T F | F | F |
| F T | T | T |
| F F | T | T |
② ~(p ∧ q) ≡ ~p ∨ ~q (드모르간 법칙)
| p q | ~(p ∧ q) | ~p ∨ ~q |
| T T | F | F |
| T F | T | T |
| F T | T | T |
| F F | T | T |
③ p → q ≡ ~q → ~p (대우 법칙)
| p q | p → q | ~q → ~p |
| T T | T | T |
| T F | F | F |
| F T | T | T |
| F F | T | T |
④ (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) (결합 법칙)
| p q r | (p ∨ q) ∨ r | p ∨ (q ∨ r) |
| T T T | T | T |
| T T F | T | T |
| T F T | T | T |
| T F F | T | T |
| F T T | T | T |
| F T F | T | T |
| F F T | T | T |
| F F F | F | F |
⑤ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) (분배 법칙)
| p q r | p ∨ (q ∧ r) | (p ∨ q) ∧ (p ∨ r) |
| T T T | T | T |
| T T F | T | T |
| T F T | T | T |
| T F F | T | T |
| F T T | T | T |
| F T F | F | F |
| F F T | F | F |
| F F F | F | F |
3) 연역적 추론
위에서 각 명제에 대한 식이 동치라는 것을 증명하기 위해 진리표라는 것을 작성했다. 하지만 위의 경우는 명제가 2, 3개 정도였지만 갯수가 4개만 되어도 16개, 5개면 32개의 행으로 진리표를 작성해야 하며 이는 매우 불편한 일이다. 그래서 이미 알고 있는 판단을 근거로 새로운 판단을 유도하는 방법을 배우게 될 것이다. 이것이 연역적 추론이다.
p → (q → r) ≡ (p ∧ q) → r 의 증명과정
p → (q → r) ≡ p → (~q ∨ r) ≡ ~p ∨ (~q ∨ r) ≡ ~(p ∧ q) ∨ r ≡ (p ∧ q) → r
(p → q) ∧ (p → r) ≡ p → (q ∧ r) 의 증명과정
(p → q) ∧ (p → r) ≡ (~p ∨ q) ∧ (~p ∨ r) ≡ ~p ∨ (q ∧ r) ≡ p → (q ∧ r)
(p → r) ∨ (q → s) ≡ (p ∧ q) → (r ∨ s) 의 증명과정
(p → r) ∨ (q → s) ≡ (~p ∨ r) ∨ (~q ∨ s) ≡ (~p ∨ ~q) ∨ (r ∨ s) ≡ ~(p ∧ q) ∨ (r ∨ s) ≡ (p ∧ q) → (r ∨ s)
2. 명제함수
C++을 해본 사람이라면 어떤 매개변수를 받아서 bool을 반환형으로 하는 함수를 한 번쯤 만들어 본 경험이 있을 것이라고 생각한다. 지금 배우려는 명제함수도 그와 매우 비슷하다고 보면 된다.
1) 명제함수와 한정기호
명제함수: 변수 x가 결정되어야 참, 거짓이 판단되는 문장 (x가 가지는 값의 범위를 대상범위 혹은 모집단이라고 부름)
한정기호: 전칭기호와 존재기호
- 전칭기호 ∀: for every (x의 범위의 전체를 대상)
- 존재기호 ∃: for some (x의 범위의 일부를 대상)
2) 명제의 부정
어떤 명제를 구성하는데 있어서 아래와 같은 기호를 사용하는 경우가 꽤 있다. 그리고 그 명제를 부정을 하는 경우가 꽤 있는데 그럴 경우에는 명제에서 사용했던 기호가 아래와 같이 바뀌게 된다. 명제 p, q가 존재한다면 두 명제 p와 q에 대해, x의 모집단은 건드리지 않도록 하며 다음 4가지 원리를 모두 사용한다.
| ∀ | ↔ | ∃ |
| ∨ | ↔ | ∧ |
| p | ↔ | ~p |
| < | ↔ | ≥ |
3. 함의와 동치
1) 항진명제와 모순명제
항진명제: 모든 논리적 가능성의 진리값들이 참인 명제 → t로 표현
모순명제: 모든 논리적 가능성의 진리값들의 거짓인 명제 → c로 표현
항진명제와 모순명제의 성질
- p ∨ ~p ≡ t
- p ∧ ~p ≡ c
- t ∨ p ≡ t
- c ∨ p ≡ p
- t ∧ p ≡ p
- c ∧ p ≡ c
위의 성질을 이용해서 아래의 명제들을 증명해보자.
① ~p → c ≡ p 의 증명
~p → c ≡ p ∨ c ≡ p
② (p → q) ∧ (q → r) → (p → r) ≡ t 의 증명 (논리에서 삼단논법, 수학에서 추이법칙으로 부름)
- (~p ∨ q) ∧ (~q ∨ r) → (~p ∨ r)
- ≡ ~((~p ∨ q) ∧ (~q ∨ r)) ∨ (~q ∨ r)
- ≡ ~(~p ∨ q) ∨ ~(~q ∨ r) ∨ (~q ∨ r)
- ≡ (p ∧ ~q) ∨ (q ∧ ~r) ∨ (~q ∨ r)
- ≡ (p ∧ ~q) ∨ ((q ∧ ~r) ∨ ~(q ∧ ~r))
- ≡ (p ∧ ~q) ∨ t ≡ t
2) 함의와 동치
함의: 항진인 조건문 p → q를 논리적 함의라 하고 p => q 로 나타내는 p는 q의 충분조건, q는 p의 필요조건이라 한다.
동치: 항진인 쌍조건문 p ↔ q를 동치 하고 p <=> q로 나타내며 p와 q는 서로의 필요충분조건이라 한다. (p ≡ q)
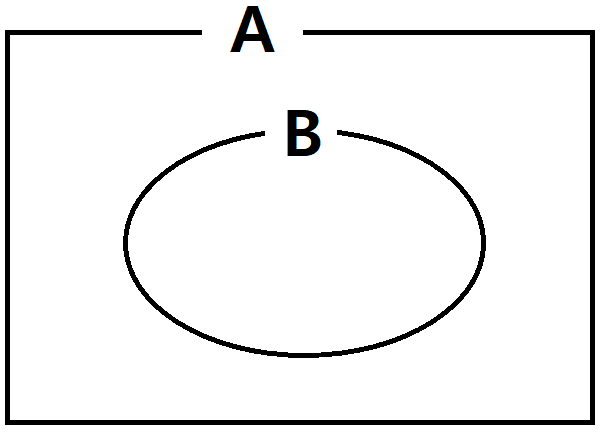
함의에 대해 더 자세히 설명하기 위해 아래의 그림을 준비했다. 아래의 그림을 의미적으로 해석하면 다음과 같다.
필요조건과 충분조건을 헷갈리는 경우가 많이 있는데 아래의 문장으로 외우면 둘을 꽤 잘 외울 수 있을 것이다. 이래도 헷갈리면 함의에서 앞의 것이 충분조건, 뒤의 것이 필요조건이라고 외우도록 하자.
- A라는 집합은 B라는 집합에 포함되기 위해 "필요"하다. → (B=>A에서 A는 필요조건)
- B라는 집합은 A라는 집합에 포함되기 "충분"하다. → (B=>A에서 B는 충분조건)
강의에서 아래의 문제를 증명했는데 이걸 하려면 고등학교에서 배운 집합에 대한 내용을 알아야 한다. 다만 까먹었다고 해서 걱정하지는 말자. 증명하는 과정이 없어서 직관적으로 받아들이는 것에 아무런 문제가 없는데다 어차피 다음 내용이 집합에 대한 내용이니 말이다. 문제는 아래와 같다.
두 명제함수 p(x), q(x)의 진리집합을 각각 P, Q라고 할 때, 다음 각 명제를 증명해보자.
p(x) => q(x) ≡ P ⊆ Q
p(x) <=> q(x) ≡ P = Q
의미적으로 해석했을 때, P이면 Q라는 것은 P가 Q의 일부를 나타낸다는 것을 이해하는 것은 자명하다. 또한 P이면 Q이고 Q이면 P일 때, P와 Q는 같다는 것은 "굳이 증명이 필요한가?" 싶을 정도로 너무나 당연해 보인다. 따라서 다음 글에서 집합에 대해 배운 후에 이를 증명해보자.
'집합론' 카테고리의 다른 글
| 이상엽 집합론 정주행 5회차 - 집합의 크기 (0) | 2023.04.12 |
|---|---|
| 이상엽 집합론 정주행 4회차 - 함수 (0) | 2023.04.06 |
| 이상엽 집합론 정주행 3회차 - 관계와 분할 (0) | 2023.04.05 |
| 이상엽 집합론 정주행 2회차 - 집합의 확장 (0) | 2023.04.03 |
| 이상엽 집합론 정주행 - Intro (0) | 2023.04.02 |